04.流水线基础和性能分析
内容概要
流水线基础
流水线概要
时空图表示
流水线分类
流水线的性能分析
流水线的吞吐率
流水线的加速比
流水线的效率
流水线基础
流水线基础：部件耗时相等的洗衣店
A, B, C, D need to wash, dry, and fold clothes
Washer takes 30 minutes
Dryer takes 30 minutes
Folder takes 30 minutes
串行工作的洗衣店(部件耗时相等)
洗衣店用 6小时完成了4个任务（0.67t/h）；
4个同学各等待了1.5小时；
Washer使用2小时；Dryer使用2小时；Folder使用2小时；
流水工作的洗衣店(部件耗时相等)
洗衣店用3小时完成了4个任务（1.33t/h）；
4个同学各等待了1.5小时；
Washer使用2小时；Dryer使用2小时；Folder使用2小时；
流水线基础：部件耗时不等的洗衣店
A, B, C, D need to wash, dry, and fold;
Washer takes 30 minutes
Dryer takes 40 minutes
Folder takes 20 minutes
串行工作的洗衣店(部件耗时不等)
洗衣店用 6小时完成了4个任务（0.67t/h）；
4个同学各等待了1.5小时；
Washer使用2小时；Dryer使用2小时40分；Folder使用1小时20分；
流水工作的洗衣店(部件耗时不等)
洗衣店用3.5小时完成了4个任务（1.14t/h）；
4个同学各等待了1.5小时；
Washer使用2小时；Dryer使用2小时40分；Folder使用1小时20分；
流水线基础：洗衣店的结论
流水线不能缩短单个任务的响应时间，但可以
提高吞吐率；流水线
速度受限于最慢流水站的速度；流水线中多个任务是
并行处理的(但任务处在不用阶段)；最大加速比 = 流水站数
流水站速度不匹配
流水线“填充”和“排空”时间
流水线基础：计算机中的流水线
流水技术及时空图
流水技术
将一重复的时序过程分解为若干子过程，每个子过程都可有效地在其 专用功能段 上与其它子过程 同时执行，这种技术称为流水技术。
流水线的表示方式：时空图
从时间和空间两个方面描述流水线的工作过程
横坐标表示时间
纵坐标表示各流水段
流水线基础：流水线的特点
流水过程由多个相关的子过程组成，这些子过程称为流水线的“级”或“段”。段的数目称为流水线的“深度”。
每个子过程由专用的功能段实现，各功能段的时间应基本相等，通常为1个时钟周期。
流水线需要经过一定的通过时间才能稳定。
流水技术适合于大量重复的时序过程。
流水线基础：流水线的分类
（1）单功能、多功能流水线
单功能流水线，是指只能完成一种固定功能的流水线。
例如：功能单元流水线，浮点加法流水线等
多功能流水线，是指各段可以进行不同的连接，从而完成不同的功能。
例如：TI ASC的多功能流水线
（2）静态、动态流水线
静态流水线，是指在某段时间间隔内，流水线的各段只能按同一种功能的连接方式工作。
例如：TI ASC的流水线，适合于处理一串相同的运算操作。
动态流水线，是指在某段时间内，当某些段正在实现某种运算时，另一些段却在实现另一种运算。
能提高流水效率，但同时会使流水线的控制变得很复杂。
（3）部件级、处理机级及处理机间流水线
部件级流水线，又叫运算操作流水线，是把处理机的算术逻辑部件分段，使得各种数据类型的操作能够进行流水。
处理机级流水线，又叫指令流水线，是把解释指令的过程按照流水方式处理。
处理机间流水线，又叫宏流水线，是由两个以上的处理机串行地对同一数据流进行处理，每个处理机完成一项任务。(如map-reduce)
注: 流水处理的粒度越来越大.
（4）标量、向量流水处理机
标量流水处理机，是指处理机不具有向量数据表示，仅对标量数据进行流水处理。
例如：IBM360/91，Amdahl 470V/6等
向量流水处理机，是指处理机具有向量数据表示，并通过向量指令对向量的各元素进行处理。
例如：TI ASC、STAR-100、CRAY-1等
（5）线性、非线性流水线
线性流水线是指流水线的各段串行连接，没有反馈回路。
非线性流水线是指流水线中除有串行连接的通路外，还有反馈回路。存在流水线调度问题：
确定什么时候向流水线引进新的输入，从而使新输入的数据和先前操作的反馈数据在流水线中不产生冲突，此即所谓 流水线调度问题。
注: 通常每个流水段执行次数不同, 为非线性流水线.
（6）顺序、乱序流动流水线
按照输出端任务流出顺序与输入端任务流入顺序是否相同划分
乱序流动流水线也可称为无序流水线、错序流水线
流水线的性能分析
流水线的吞吐率
吞吐率是指单位时间内流水线所完成的任务数或输出结果的数量(指令数)。
最大吞吐率TP_max是指流水线在达到稳定状态后的吞吐率。
设流水线由m段组成，完成n个任务的吞吐率称为实际吞吐率，记作TP。
最大吞吐率
假设流水线各段的时间相等，均为△t0，则：
TPmax = 1/△t0
假设流水线各段时间不等，第i段时间为△ti ，则：
TPmax = 1/max{△ti}
最大吞吐率取决于流水线中最慢一段所需的时间，该段成为流水线的瓶颈。
消除流水线瓶颈方法
注: 消除流水线瓶颈方法有 细分瓶颈段 和 重复设置瓶颈段.
流水线的吞吐率 (各段相等)
实际吞吐率TP：小于最大吞吐率。
第一种情况：各段时间相等（设为△t0）假设流水线由 m 段组成，n 个任务；
完成 n 个任务所需的时间：
T_流水 ＝m△t0 ＋(n－1)△t0
注: m△t0称为注入时间(filling time).
实际吞吐率TP
TP < TP_max
n >> m 时，TP ≈ TP_max
流水线的吞吐率 (各段不等)
完成 n 个任务所需的时间
T流水 = ∑△t_i ＋(n－1)△t_j, △t_j = max{△t_i}
注: T = 各个段所加时间(头尾) + (n-1)*最长时间段.
实际吞吐率
TP < TP_max
流水线的加速比
加速比是指流水线的速度与等功能非流水
线的速度之比。
S＝T非流水 ／T流水
其中T流水 和T非流水 分别为按流水和按非流水方式处理 n 个任务所需的时间
若流水线为 m 段，且各段时间相等，均为△t0 ，则：
T非流水 ＝n m△t0
T流水 ＝m△t0 ＋(n－1)△t0
非流水方式所需时间
流水线的加速比
当n >> m 时，S ≈ m
流水线的效率
效率（E）指流水线的设备利用率。
由于流水线有通过时间和排空时间，所以流水线的各段并非一直满负荷工作，即：E<1。
若各段时间相等，则各段效率也相等，即
e1 = e2 = e3 =… = n△t0/T流水
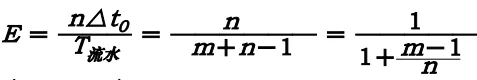
n >> m, E≈1
从时空图上看，效率就是n个任务所占的时空区与m个段总的时空区之比。
根据这个定义，可以计算流水线各段时间
不等时的流水线效率：
从时空图看流水线的效率
流水线性能示例
例:（张晨曦教材） 在下面所示的静态流水线上 计算： SUM(A1B1:A4B4)，求：吞吐率、加速比、和效率。
此类问题的一般解决步骤：
根据目标公式确定计算过程
根据1中确定的计算过程画时空图
根据2中给出的时空图计算性能
① 确定计算过程
② 画出时空图
③ 根据时空图计算性能
流水线性能总结
流水线并不能减少（而且一般是增加）单条指令的执行时间，但能够提高吞吐率；
增加流水线的深度通常可以提高流水线性能；
流水线深度受限于流水线的延迟和额外开销；
流水线的额外开销包括：
流水寄存器的延迟
建立时间：触发写操作的信号到达前寄存器输入保持稳定
的时间；
传输延迟：时钟信号到达后到寄存器输出可用的时间；
时钟扭曲
时钟信号到达各流水寄存器的最大差值时间；
Last updated
