> For the complete documentation index, see [llms.txt](https://dolorhunter.gitbook.io/w3notepad/llms.txt). Markdown versions of documentation pages are available by appending `.md` to page URLs; this page is available as [Markdown](https://dolorhunter.gitbook.io/w3notepad/computerarchitecture/chep2.md). # 02.Performance Analysis ## 性能分析 Which of the following airplanes has the best performance? | Airplane | Passengers | Range (mi) | Speed (mph) | | ---------------- | ---------- | ---------- | ----------- | | Boeing 737-100 | 101 | 630 | 598 | | Boeing 747 | 470 | 4150 | 610 | | BAC/Sud Concorde | 132 | 4000 | 1350 | | Douglas DC-8-50 | 146 | 8720 | 544 | * How much faster is the Concorde vs. the 747? (Speed) * How much bigger is the 747 vs. DC-8? (Passengers) Which computer is the fastest? The answer is not simple: * Scientific simulation - FP performance * Program development - Integer performance * Database workload - Memory, I/O ## 计算机的性能 Want to buy the fastest computer for what you want to do? * `Workload` is very important * Correct measurement and analysis method Want to design the fastest computer for what the customer wants to pay? * Cost is an important criterion(标准) ## 本节内容 * Time and performance * Iron Law —> Time * MIPS and MFLOPS * Which programs and how to average * Amdahl’s law ## 如何定义性能 What is important to whom? Computer system user * Minimize elapsed time for program: `t_resp = t_end - t_start` * Called `response time (响应时间)` Datacenter manager * Maximize completion rate = #jobs/second * Called `throughput (吞吐率)` ## Response Time vs. Throughput Is throughput = 1/avg. response time? * Only if `NO` overlap * Otherwise, throughput > 1/avg. response time * 举例：A lunch buffet (自助餐) * Assume 5 entrees (主菜) * Each person takes 2 minutes/entree * Throughput is 1 person every 2 minutes * BUT time to fill up tray (盘子) is 10 minutes * Why and what would the throughput be otherwise? * 5 people simultaneously filling tray (overlap) * Without overlap, throughput = 1/10 ## 对于计算机，什么是性能 * For computer architects * CPU time = time spent running a program * Intuitively, `bigger should be faster`, so: * Performance = 1/X time, where X is response, CPU execution, etc. * Elapsed time(经过时间) = CPU time + I/O wait * `We will concentrate on CPU time` ## 如何提升性能 Improve (a) response time or (b) throughput? * A Faster CPU * Helps both (a) and (b) * Add more CPUs * Helps (b) and perhaps (a) due to less queueing ## 如何比较性能 * Machine A is n times faster than machine B iff : * perf(A)/perf(B) = time(B)/time(A) = n * Machine A is x% faster than machine B iff * perf(A)/perf(B) = time(B)/time(A) = 1 + x/100 * 举例：time(A) = 10s, time(B) = 15s * 15/10 = 1.5 => A is 1.5 times faster than B * 15/10 = 1.5 => A is 50% faster than B ## How to obtain the time 方法：通过分解指令 * Breaking program into instructions * HW is aware of instructions, not programs * At lower level, H/W breaks instructions into cycles * Lower level state machines change state every cycle * For example: * 1GHz Snapdragon runs 1000M cycles/sec, 1 cycle = 1ns * 2.5GHz Core i7 runs 2.5G cycles/sec, 1 cycle = 0.25ns ## 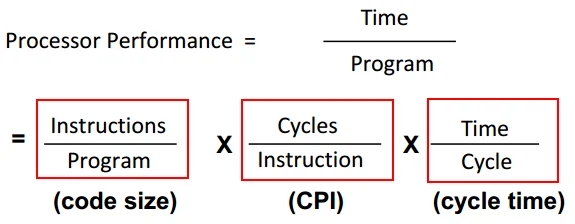Iron Law in Performance ![Iron Law in Performance](https://res.cloudinary.com/dfb5w2ccj/image/upload/v1588142448/notepad/2020-04-29_143917_q0mysg.webp) Architecture —> Implementation —> Realization Compiler Designer | Processor Designer | Chip Designer * Instructions/Program * Instructions executed, not static code size(程序有循环, 分支) * Determined by algorithm, compiler, ISA * Cycles/Instruction * Determined by ISA and CPU organization * Overlap among instructions reduces this term * Time/cycle * Determined by technology, organization, clever circuit design ## 设计的目标 * Minimize time which is the product, `NOT` the isolated terms * Common error to miss terms while devising optimizations * E.g. ISA change to decrease instruction count * BUT leads to CPU organization which makes clock slower * Be mind that: `terms are inter-related` ## 其它指标 * MIPS: 每秒百万次整型操作 ``` MIPS = instruction count / (execution time x 10^6) = clock rate / (CPI x 10^6) ``` * `But MIPS has serious shortcomings` MIPS的问题(示例) E.g. without FP hardware, an FP op may take 50 single-cycle instructions. With FP hardware, only one 2-cycle instruction * Thus, adding FP hardware: * CPI increases (why?) `50/50 => 2/1` (变差了, CPI越小越好.) * Instructions/program decreases (why?) `50 => 1` * Total execution time decreases `50 => 2` * BUT, MIPS gets worse! `1 MIPS => 0.5 MIPS` MIPS的问题(根源) * Ignores program * Usually used to quote peak performance * Ideal conditions => guaranteed not to exceed! * When is MIPS ok? * Same compiler, same ISA * E.g. same binary running on AMD Jaguar, Intel Core i7 * Why? `Instr/program is constant and can be factored out` 其它指标 * MFLOPS = FP ops in program / (execution time x 10^6) * Assuming FP ops independent of compiler and ISA * Often safe for numeric codes: matrix size determines # of FP ops/program * However, not always safe: * Missing instructions (e.g. FP divide) * Optimizing compilers ## 性能分析的主要原则 `能用时间尽量用时间, 如果绝对时间拿不到, 用相对时间 / 归一化时间也可以.` * Use `ONLY` Time * Beware when reading, especially if details are omitted * Be careful when you buy products * Beware of Peak * “Guaranteed not to exceed” ## Iron Law Example A: * Machine A:clock 1ns, CPI 2.0, for program x * Machine B: clock 2ns, CPI 1.2, for program x * Which machine is faster and how much? `Ans:` ``` Time/Program = instr/programx cycles/instrx sec/cycle Time(A) = N x 2.0 x 1 = 2N Time(B) = N x 1.2 x 2 = 2.4N Compare: Time(B)/Time(A) = 2.4N/2N = 1.2 ``` So, Machine A is 20% faster than Machine B for program x B: Keep clock(A) @ 1ns and clock(B) @2ns To get equal performance: if CPI(B)=1.2, what should CPI(A) be? `Ans:` ``` Time(B) / Time(A) = 1 = (Nx2x1.2) / (Nx1xCPI(A)) => CPI(A) = 2.4 ``` C: * Keep CPI(A)=2.0 and CPI(B)=1.2 * For equal performance: if clock(B)=2ns, what should clock(A) be? 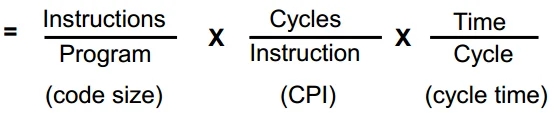`Ans:` ``` Time(B)/Time(A) = 1 = (N x 2.0 x clock(A))/(N x 1.2 x 2) => clock(A) = 1.2ns ``` ## 总结一 * Time and performance: Machine A n times faster than Machine B * `Iff Time(B)/Time(A) = n` * Iron Law: Performance = Time/program = ![Iron Law](https://res.cloudinary.com/dfb5w2ccj/image/upload/v1588144568/notepad/2020-04-29_151516_ytzb2z.webp) * Other Metrics: MIPS and MFLOPS * Beware of peak and omitted details ## 怎么衡量不同机器的性能 * Execution time of what program? * Best case - you always run the same set of programs * Port them and `time the whole workload` * In reality, use benchmarks(基准测试) * Programs chosen to measure performance * Predict performance of actual workload * Saves effort and money `Representative? Honest? Benchmarketing..` 如何表示性能(用单个数值） | - | Machine A | Machine B | | --------- | --------- | --------- | | Program 1 | 1 | 10 | | Program 2 | 1000 | 100 | | Total | 1001 | 110 | For total execution time, how much faster is B? ``` 1001 / 110 = 9.1x ``` How to Average? ## Arithmetic Mean * Arithmetic Mean (same result) ![Arithmetic Mean](https://res.cloudinary.com/dfb5w2ccj/image/upload/v1588145222/notepad/2020-04-29_152451_mcvci4.webp) * Arithmetic mean of times: * AM(A) = 1001/2 = 500.5 * AM(B) = 110/2 = 55 * Speedup: 500.5/55 = 9.1x * Valid only if programs run `equally often`, so use weighted arithmetic mean: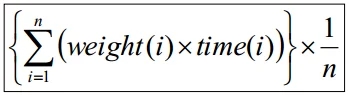 ![Weighted Arithmetic Mean](https://res.cloudinary.com/dfb5w2ccj/image/upload/v1588145222/notepad/2020-04-29_152535_jd7dyh.webp) `How to determine the weight?` Problem of AM * E.g., 30 mph for first 10 miles, then 90 mph for next 10 miles, what is average speed? * Average speed = (30+90)/2 ??? `WRONG` ``` Average speed = total distance / total time = (20 / (10/30 + 10/90)) = 45 mph ``` ## Harmonic Mean * Harmonic mean(谐波均值) of rates = ![Harmonic Mean](https://res.cloudinary.com/dfb5w2ccj/image/upload/v1588145593/notepad/2020-04-29_153142_ln0ht0.webp) * `Use HM if forced to start and end with rates (e.g. reporting MIPS or MFLOPS)` * Why? * Rate has time in denominator * Mean should be proportional to inverse of sums of time (not sum of inverses) * See: J.E. Smith, “Characterizing computer performance with a single number,” CACM Volume 31 , Issue 10(October 1988), pp. 1202-1206. Dealing with Ratios | - | Machine A | Machine B | | --------- | --------- | --------- | | Program 1 | 1 | 10 | | Program 2 | 1000 | 100 | | Total | 1001 | 110 | If we take ratios with respect to machine A | - | Machine A | Machine B | | --------- | --------- | --------- | | Program 1 | 1 | 10 | | Program 2 | 1 | 0.1 | | Average | 1 | 5.05 | ``` Avg. wrt. 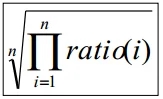machine A: A is 1, 5.05 ``` If we take ratios with respect to machine B | - | Machine A | Machine B | | --------- | --------- | --------- | | Program 1 | 0.1 | 1 | | Program 2 | 10 | 1 | | Average | 5.05 | 1 | `Can’t both be true!!!` `Don’t use arithmetic mean on ratios!` *注: 对于相对 / 归一化的数据, 不使用均值计算, 用几何均值.* ## Geometric Mean * Use geometric mean for ratios * Geometric mean of ratios = ![Geometric Mean](https://res.cloudinary.com/dfb5w2ccj/image/upload/v1588145593/notepad/2020-04-29_153233_bl44zs.webp) * `Independent of reference machine` * In the example, GM for machine a is 1, for machine B is also 1 * Normalized(归一化) with respect to either machine Disadvantage * `GM of ratios is not proportional to total time`(GM计算时会消去时间) * AM in example says machine B is 9.1 times faster * GM says they are equal * If we took total execution time, A and B are equal only if * Program 1 is run 100 times more often than program 2 * `Generally, GM will mispredict for three or more machines` ## 总结二 * Use AM for times * Use HM if forced to use rates * Use GM if forced to use ratios `Best of all, use unnormalized numbers to compute time` ## 基准测试: SPEC2000 * System Performance Evaluation Cooperative * Formed in 80s to combat benchmarketing * SPEC89, SPEC92, SPEC95, SPEC2000, SPEC2006 * Latest one is SPEC2017 * 12 integer and 14 floating-point programs * Sun Ultra-5 300MHz reference machine has score of 100 * Report `GM of ratiosto` reference machine Benchmark Pitfalls * Benchmark not representative * Your workload is I/O bound, SPEC is useless * Benchmark is too old * Benchmarks age poorly; benchmarketing pressure causes vendors to optimize compiler, hardware, software to match benchmarks * Need to be periodically refreshed ## Amdahl’s Law `加速比 = 未优化时间 / 优化后时间` * Motivation for `optimizing common case` * Speedup = old time / new time = new rate / old rate * Let an optimization speed fraction f of time by a factor of s ``` New_time = (1-f) x old_time + (f/s) x old_time Speedup = old_time / new_time Speedup = old_time / ((1-f) x old_time + (f/s) x old_time) ``` ![Amdahl’s Law](https://res.cloudinary.com/dfb5w2ccj/image/upload/v1588147466/notepad/2020-04-29_155725_sa0ajz.webp) *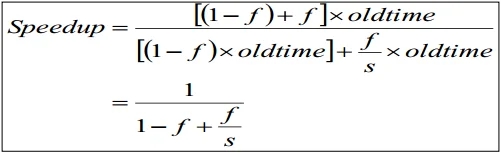注: f为加速时间占总时间的比例, (1-f)为不可加速时间比例, (f/s)为可加速时间比例.* Example of Amdahl’s Law Your boss asks you to improve performance by: * Improve the ALU used 95% of time by 10% * Improve memory pipeline used 5% of time by 10x ![Amdahl’s Law](https://res.cloudinary.com/dfb5w2ccj/image/upload/v1588147465/notepad/2020-04-29_160331_ezamah.webp) | 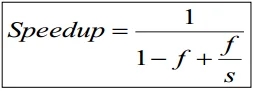f | s | Speedup | | --- | ---- | ------- | | 95% | 1.10 | 1.094 | | 5% | 10 | 1.047 | | 5% | ∞ | 1.052 | *注: 说明 optimizing common case 很重要.* Limitation of Amdahl’s Law Make common case fast: ![Limitation of Amdahl’s Law](https://res.cloudinary.com/dfb5w2ccj/image/upload/v1588147857/notepad/2020-04-29_161004_b1eckh.webp) ![Limitation of Amdahl’s Law](https://res.cloudinary.com/dfb5w2ccj/image/upload/v1588147857/notepad/2020-04-29_160926_o00hsl.webp) * 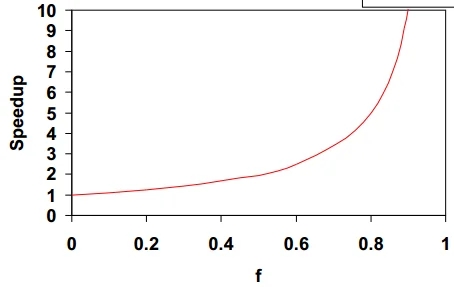Consider uncommon case! * If (1-f) is nontrivial * Speedup is limited! * Particularly true for exploiting parallelism in the large, where large s is not cheap * GPU with e.g. 1024 processors (shader cores) * Parallel portion speeds up by s (1024x) * Serial portion of code (1-f) limits speedup E.g. 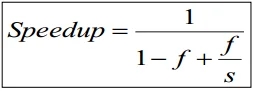10% serial portion: 1/0.1 = 10x speedup with 1000 cores ## 总结三 * Benchmarks: SPEC2000 * Summarize performance: * AM for time * HM for rate * GM for ratio * Amdahl’s Law: ![Amdahl’s Law](https://res.cloudinary.com/dfb5w2ccj/image/upload/v1588147465/notepad/2020-04-29_160331_ezamah.webp)